From Characters to Tokens: Dynamic Grouping with Hierarchical BPE
Published:
Transformers work particularly well with sub-word tokenisations, which improve model quality and shorten sequences for faster inference. However, the gains taper off once the vocabulary becomes very large (> 500K): many tokens are rare, their embeddings are under-trained, and the bloated embedding matrix adds cost without proportional benefit. At the other end of the spectrum, character-level models avoid the rare-token problem by construction, but their sequences are much longer; with standard self-attention’s quadratic time and memory, this often makes them impractical.
Recent hierarchical approaches aim to reconcile character-level robustness with subword-level efficiency by grouping characters into patches. However, existing patching strategies often depend on whitespace-restricting applicability to languages without clear word boundaries-or require auxiliary models that introduce additional complexity and dependencies.
We propose a dynamic character-grouping method that leverages the structure of standard BPE tokenisation without auxiliary models. Specifically, we append explicit end-of-patch markers to BPE tokens and apply a second, lightweight BPE pass to regulate patch granularity. This design yields representations that are efficient, flexible, and language-agnostic, while preserving a simple training and deployment pipeline.
Algorithm: Dynamic Patching with Two-Stage BPE
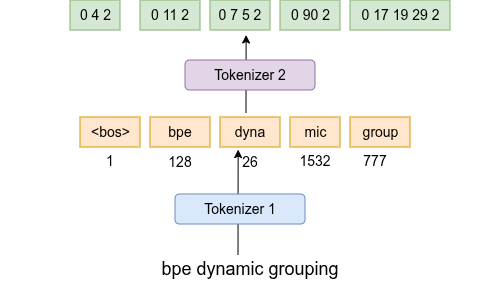
Figure 1 provides a schematic overview. Below is the procedure in a compact format.
Notation
| Symbol | Meaning |
|---|---|
T₁ | Existing subword tokenizer (BPE; “Tokenizer 1”) |
<!> | End-of-patch marker (EoP) appended to every T₁ token |
T₂ | Lightweight, inner BPE (“Tokenizer 2”) applied within each patch |
S | Maximum sub-token length per patch after T₂ (small cap, e.g. 4–8) |
E_local / D_local | Local encoder/decoder operating inside each patch |
E_global | Global causal Transformer over patch embeddings |
c | Raw character stream |
pᵢ | i-th patch (characther of a T₁ token + <!>) |
zᵢ | Patch embedding produced by E_local |
High-Level Idea (TL;DR)
- Start from any existing BPE (
T₁). Each token becomes a patch. - Append an end-of-patch marker
<!>so decoding is incremental. - Apply a lightweight BPE (
T₂) inside each patch to cap length at a smallS. - Use local encoders/decoders per patch + a global causal Transformer over patch embeddings.
- Outcome: faster models and state-of-the-art BPB among dynamic patching baselines—without a boundary model and without whitespace assumptions.
- More details about the local and global models can be found in the architecture section.
Procedure
Outer tokenisation (patching).
Tokenise text withT₁to obtain[t₁, t₂, …, t_N].
For eachtᵢ, form a patch of characthers within the token:pᵢ = (c_1^i, c_2^i, ..., c_L^T <!>).Within-patch compression.
For eachpᵢ, applyT₂to obtain a bounded sequence
uᵢ = T₂(pᵢ)with|uᵢ| ≤ S.Local encoding.
EncodeuᵢwithE_localto produce a fixed-size embeddingzᵢ.Global modelling.
Feed the sequence[z₁, z₂, …, z_N]toE_global(causal Transformer) for autoregressive modelling over patches.Decoding (incremental).
During generation,E_globalpredicts the next patch representation;
D_localdecodesuᵢ → pᵢ, then strip the EoP⟂to recovertᵢand characters.
Architecture
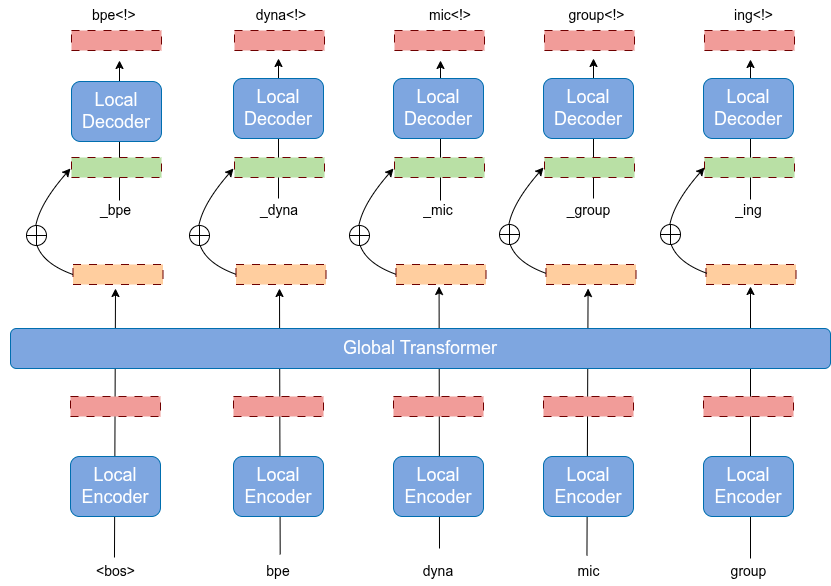
- Local encoder: turns each bounded-length patch into an embedding.
- Global Transformer: models the sequence of patch embeddings (short!).
- Local decoder: reconstructs the next patch internally during training/inference.
Why it’s efficient: replacing a huge embedding matrix with light local modules + shorter global sequences reduces FLOPs and parameters while improving bits-per-byte (BPB).
Results (high level)
- Lower BPB than standard BPE and entropy-based patching; competitive with space-based patching without relying on spaces.
- Compact models: fewer parameters than BPE baselines yet better compression (lower BPB).
- Language-agnostic: strong results on non-whitespace scripts (e.g., Chinese).
- Patch sizes ~4 bytes in practice → short global sequences and faster compute.
Table 1 — Comparison for S = 10, BPE tokenisation, Space and Entropy patching (Ent.-Patch, Ent.-Space) for 128M models trained for 13,500 steps. FLOPs are in billions. “” denotes the unbounded model. We report the mean over multiple runs on the test set; max std dev across experiments: ±0.007.*
| Model | FLOPs↓ | Fertility↓ | Params | BPB↓ |
|---|---|---|---|---|
| Ent.-Patch* | 509 | 1.41 | 351M | 1.24 |
| Ent.-Patch | 668 | 1.83 | 351M | 1.20 |
| Space-Patch | 534 | 1.451 | 351M | 1.14 |
| Char - Level | 4214 | 4.5 | 85M | 1.16 |
| BPE | 562 | 1.51 | 123M | 1.16 |
| BPE-Patch | 554 | 1.51 | 99.7M | 1.11 |
Table 2 shows that our approach outperforms all baselines in this setup. The entropy-patching method yields the weakest results, likely due to a domain mismatch between its entropy model’s training data and SlimPajama. Although the unbounded entropy variant is more FLOP-efficient, its longer patches force the local models to learn more complex representations with limited capacity, causing a marked drop in performance. Constraining the maximum patch length to 6 improves accuracy, but at higher FLOPs-and it still trails our method.
Space-based patching is the most FLOP-efficient baseline and reasonably strong, yet it fails to generalise to languages without whitespace, an issue our method avoids. Character-level modelling uses fewer parameters but is both slower and less predictive. Notably, we also surpass standard BPE despite using fewer parameters, suggesting our local encoders learn richer token-level representations than a fixed embedding matrix.
Downstream evaluation
To further verify our model, we conduct experiments on question-answering tasks. We first pre-train a medium model on next-token prediction for 15B tokens, then perform zero-shot evaluations on:
- Commonsense Reasoning (0-shot): HellaSwag Zellers et al., 2019, PIQA Bisk et al., 2020, WinoGrande Sakaguchi et al., 2020, and ARC-e/-c Clark et al., 2018.
- Broad Context Understanding: LAMBADA (OpenAI) Paperno et al., 2016.
- Popular Aggregated Results: MMLU Hendrycks et al., 2021.
To obtain the scores, we compute the log-likelihood per character within each patch and select the answer with the highest log-likelihood. Table 2 shows that we outperform the standard BPE approach and entropy-based patching, while performing on par with space patching on most benchmarks. We also evaluate language-modelling capacity via BPB: as shown in Table 2, the medium model improves with scale (lower BPB than the small model) and outperforms other baselines at larger sizes.
Table 2: Common Academic Evaluation Benchmarks comparing a standard embedding matrix vs. our learnable embeddings. Task performance is zero-shot.
| Model | Param | MMLU (acc) | Hella (acc_norm) | Lmb. (acc) | ARC-c (acc_norm) | ARC-e (acc) | Wino. (acc) | Piqa (acc) |
|---|---|---|---|---|---|---|---|---|
| BPE | 359M | 23.00 | 31.3 | 29.89 | 23.63 | 38.05 | 50.5 | 61.43 |
| Ent.-Patch | 575M | 23.07 | 32.91 | 29.40 | 20.90 | 36.60 | 48.8 | 59.60 |
| Space-Patch | 575M | 23.24 | 35.9 | 32.8 | 21.50 | 39.02 | 52.5 | 64.2 |
| BPE-Patch | 323M | 22.90 | 34.6 | 32.5 | 22.10 | 40.6 | 53.4 | 63.3 |
| BPE-Patch | 1.3B | 24.95 | 52.3 | 47.3 | 28.1 | 52.2 | 54.9 | 70.1 |
Practical tips
- Cap S around 8–10 for a sweet spot between speed and fidelity.
- Works with any BPE (GPT-2, LLaMA-3/SPM, etc.).
- Drop the auxiliary boundary network used in entropy patching the end marker is enough.
```
We enforce the maximum space size to be 6, resulting in a fertility higher than 1. ↩
